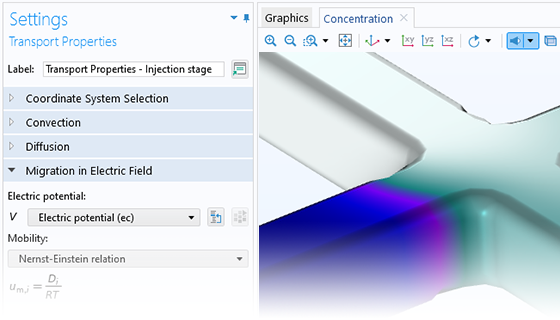
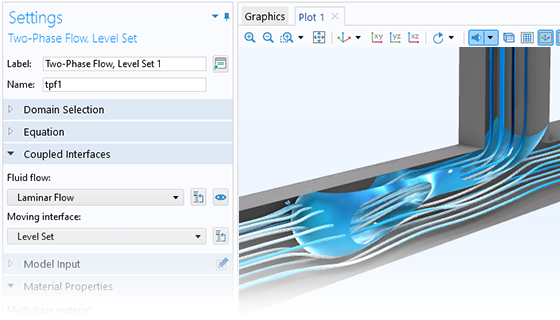
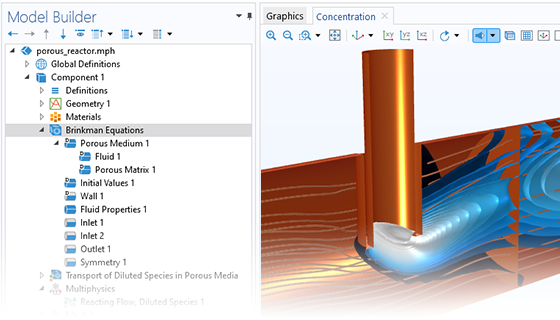
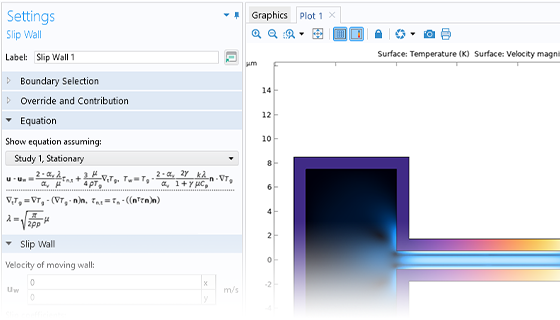
Describe Fluids at the Microscale
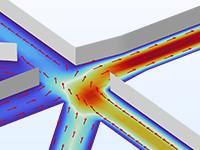
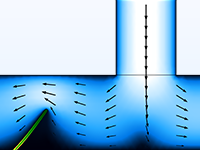
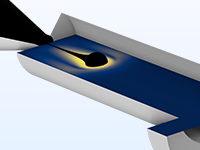
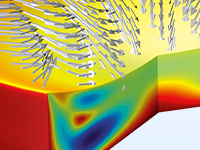
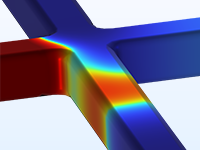
Microfluidic flows occur on length scales that are orders of magnitude smaller than macroscopic flows. Manipulation of fluids at the microscale has a number of advantages; because they are smaller, microfluidic systems typically operate faster and require less fluid than their macroscopic equivalents.
Energy inputs and outputs (for example, heat generated in a chemical reaction) are also easier to control because the surface-to-area volume ratio of the system is much greater than that of a macroscopic system. In general, as the length scale of the fluid flow is reduced, properties that scale with the surface area of the system become comparatively more important than those that scale with the volume of the flow.
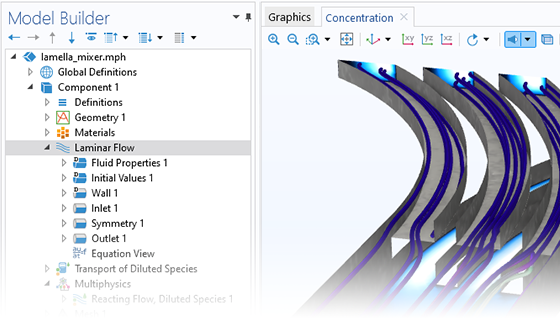
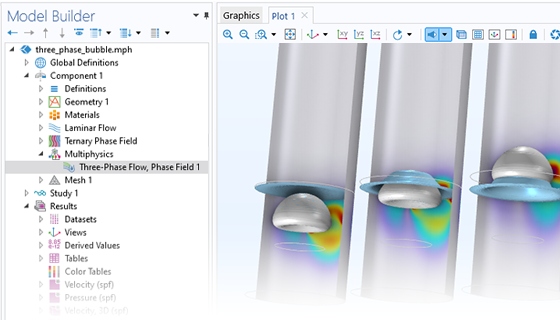
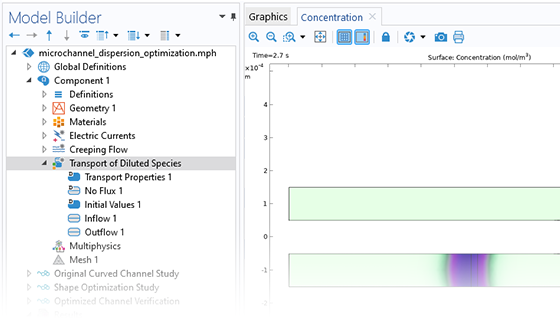
The Microfluidics Module is designed specifically for handling momentum, heat, and mass transport with special considerations for fluid flow at the microscale.