Modeling Metamaterials with a Time-Domain Perfectly Matched Layer Formulation
INTRODUCTION: Perfectly matched layers (PML) have been widely used for simulating wave propagation in unbounded media to effectively avoid spurious wave reflections from the computational domain boundaries. Time-domain PML formulations, especially for elastic waves, usually use a complex system of first-order equations.
Compact second-order time-domain formulations are particularly desired for finite element method (FEM) simulations in COMSOL Multiphysics® software. Such PML formulations were introduced by the authors [1, 2] for modeling wave propagation in unbounded fluid, solid, as well as for coupled fluid-solid media. In this work, we demonstrate the use of a time-domain PML formulation for the complex case of wave propagation in acoustic/elastic metamaterials. In particular, the time-domain superfocusing of acoustic waves in water by a slab of a solid metamaterials lens (see Zhou et al. [3]) is presented, enabling many interesting characteristics of metamaterials to be observed. The limitations of the PML in modeling metamaterials will be addressed, particularly the use of periodic structures within the PML, as considered in [4].
USE OF COMSOL MULTIPHYSICS: Our PML formulations were reformulated in a weak form to facilitate the use of the mathematical models using the PDE interfaces in the COMSOL software. The fluid-solid coupling boundary conditions were presented in a form that enables these conditions to be easily integrated into the weak formulation. Second order Lagrange finite elements were used for space discretization, while the generalized alpha method was used for time discretization.
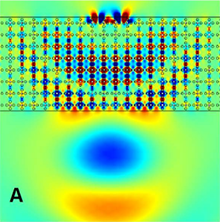
RESULTS: The solid metamaterial lens proposed by Zhou et al. [3], was used in our simulations. It consists of a periodic structure of brass cylinders and cavities embedded in Al-SiC foam, with a unit cell as shown in the top right panel of Figure 1. The left column of Figure 1 shows snapshots of the simulations for the case were the slab of solid consists only of the foam matrix with water on both sides, while the right column shows the corresponding snapshots when the metamaterial periodic structure is included, but well within the physical domain. The very slow group velocity, reversed phase velocity, and other theoretically expected properties of metamaterials are observed in the simulations. Figure 2 shows results corresponding to those of Figure 1, but with the periodic structure extending to the inner edge of the PML. The way the total energy evolves in time within the solid slab is presented in Figure 3 for the three simulations in the first two figures. Figure 4 shows the simulations for the case where the periodic structure extends inside the PML. It is clear that the solution blow up marking a limitation of the PMLs in this case.
CONCLUSION: The use of compact second-order time-domain formulations in modeling the complex and interesting case metamaterials, which are usually modeled in frequency domain, is presented. The limitation of the PML in the case of periodic metamaterials is addressed. Some proposed future work to overcome these limitations for periodic and homogenized metamaterials will be discussed.
Download
- assi_presentation.pdf - 4.18MB
- assi_abstract.pdf - 2.23MB
