In corrosion analysis, we often want to study corroding surfaces whose electrical connectivity is not as simple as a controlled current or voltage. Instead, an electrode surface might be short circuited to another electrode through a direct connection or through a resistor, such as for the electrical connection between a monopile and transition piece in an offshore wind turbine fundament. Here, we look at how to describe these electrodes and external short circuits using the appropriate boundary conditions in the COMSOL Multiphysics® software.
Sacrificial Anode Cathodic Protection in Corrosion Analyses
The phenomenon of galvanic corrosion is exploited intentionally in sacrificial anode cathodic protection. To protect a structural component (usually steel) from corroding, it is electrically connected to a sacrificial anode made of a less noble metal. The sacrificial anode then corrodes preferentially. Note that in order for the sacrificial anode to protect the steel effectively, there needs to be a direct electrical connection between the two metals to close the electrical circuit. In effect, the sacrificial anodes are short circuited to the protected surface so that they start to corrode.
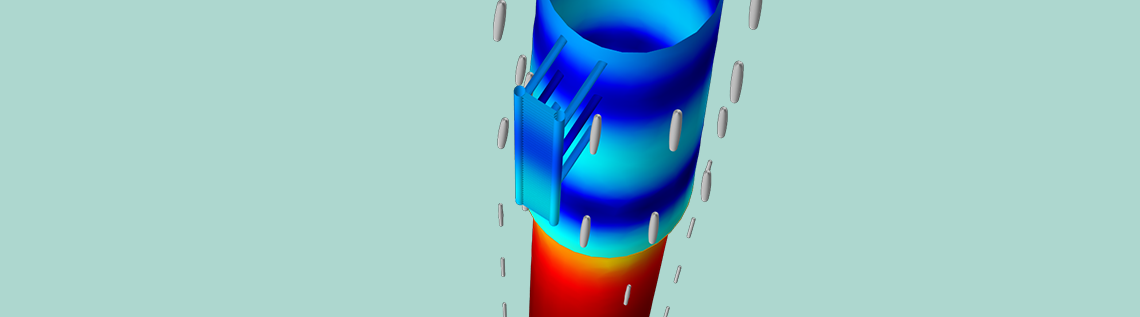
When we define sacrificial anodes in a COMSOL Multiphysics model, we can usually assume that the anode material and the cathode material are good electrical conductors. Thus, the electric potential can be set uniformly to 0 V on both the sacrificial anode and protected steel surfaces. Below, we see an analysis of a steel platform taken from the Anode Film Resistance Effect on Cathodic Protection tutorial. In this model, we define the steel surface with the same external electric potential condition as for the sacrificial anodes.
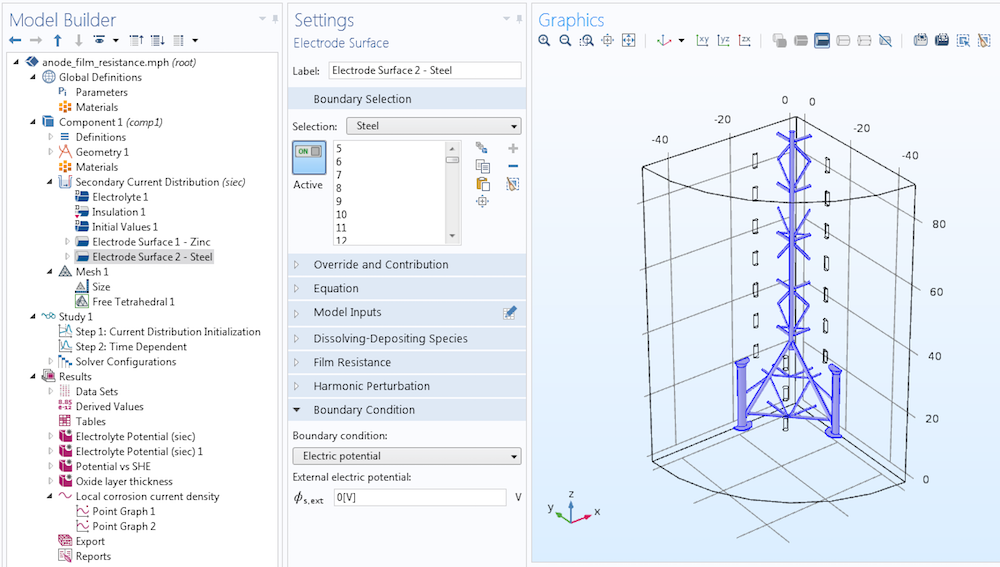
The Electrode Surface boundary condition applies an external electric potential of 0 V to the steel surface. The same condition with a more negative corrosion potential causes the sacrificial anodes to corrode.
Modeling Electrodes and External Short Circuits in COMSOL Multiphysics®
What if the electrical contact between two metal surfaces is not ideal? For example, they might be linked by cables that have an appreciable electrical resistance. Rather than setting the electric potential directly to 0 V, we use the External Short boundary condition. This setting defines the external electric potential on an electrode surface as a uniform floating potential that is connected to ground by a series resistance. The exact value of the voltage versus ground depends on the total current being drawn at the electrode surface, according to Ohm’s law.
Let’s look at an example: A common task in offshore cathodic protection is the protection of monopiles. These are the steel foundations used to secure offshore structures, such as wind turbine towers in a seabed. Typically, a monopile is structurally connected to a transition piece. While the monopile is always below the water surface, the transition piece extends above it.
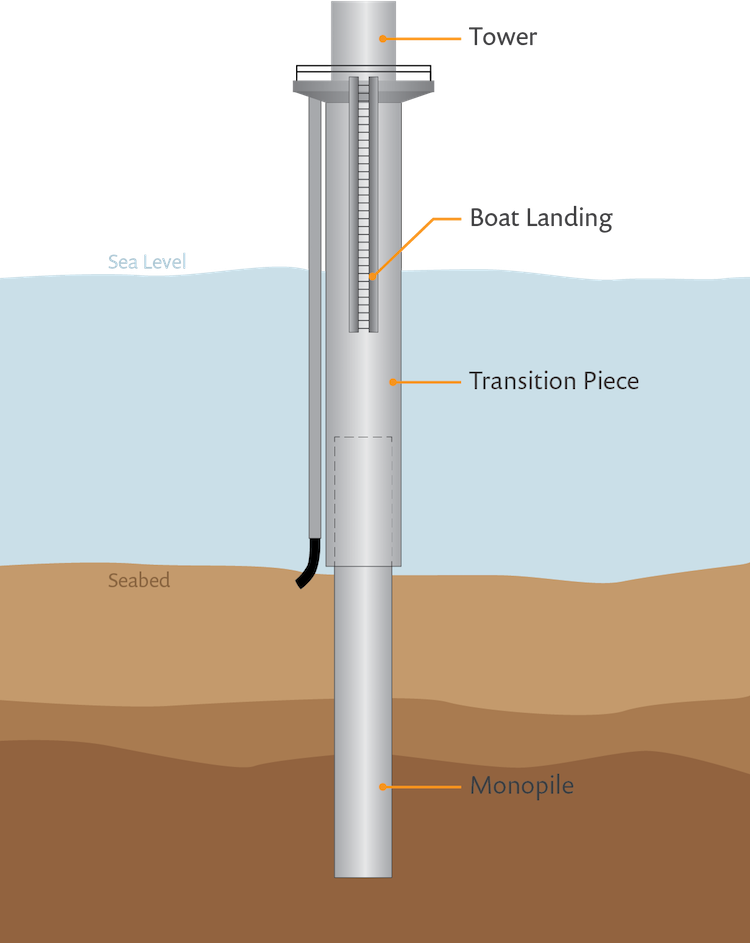
A schematic of a typical offshore monopile structure.
To protect all of the structural steel parts from corrosion, we use several sacrificial anodes mounted onto the transition piece. When the anodes have a direct electrical connection only to the transition piece, the monopile stays protected through the electrical contact it makes via structural contact. As this is not electrically ideal, we use a resistance in the electrochemical model to account for the imperfect electrical connection. We can see an example of this in our Monopile with Dissolving Sacrificial Anodes tutorial model.
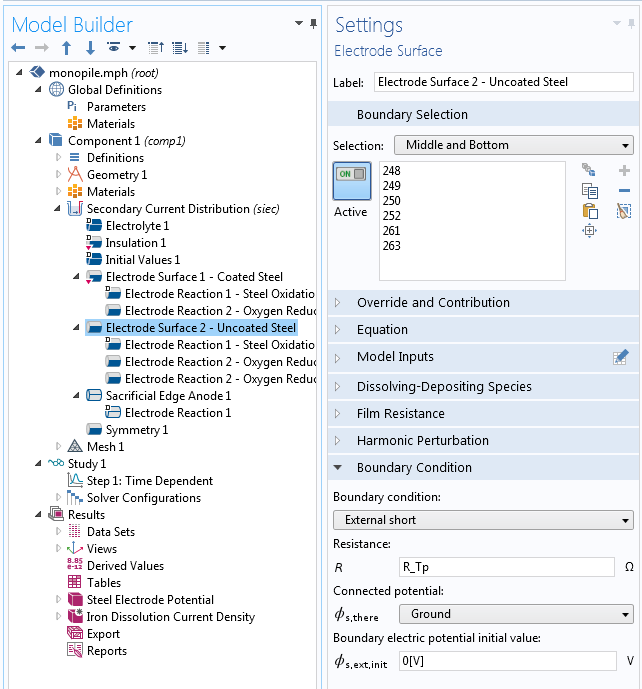
The Electrode Surface boundary condition applies an external short to ground for a monopile’s uncoated steel surface.
The External Short boundary condition links the steel surface to ground (0 V), the electric potential of the transition piece, and sacrificial anodes. Between the ground and the monopile, we apply a resistance R_Tp with a value of 0.01 Ω. This represents the resistance of the electrical contact between the monopile and transition piece.
While this isn’t a large resistance, including it is very important in this case. The total current drain on the sacrificial anodes that protect the steel surface may be tens of A, so the corresponding loss to resistance can be more than 100 mV. Since the electrochemical properties of a steel surface change from being well protected to poorly protected over a potential range of 100 mV or less, these magnitudes are comparable.
The figure below shows the external electric potential on the different parts of the surface.

The external electric potential on a transition piece (top) and monopile (bottom) surrounded by a jacket of sacrificial anodes.
Note that the electric potential is uniform on both surfaces, as they are highly conductive metals. Still, there is a potential difference of more than 140 mV between the monopile and transition piece because of the resistance included in the External Short boundary condition. This means that the steel surface is generally less well protected, which is also shown in the following plot of the electrode surface potential.

The electrode surface potential in a transition piece (top) and monopile (bottom) surrounded by a jacket of sacrificial anodes.
The blue color indicates negative (cathodic) potential, so the transition piece is relatively well protected. In comparison, the monopile surface is poorly protected and might be a corrosion risk.
The analysis with the External Short boundary condition ensures that the model correctly considers the contribution of resistance between the two structural parts. These results demonstrate that we need to be very careful when placing the anodes on the transition piece. If the cathodic protection system is poorly designed, connecting sacrificial anodes only to the transition piece might not provide adequate protection to the monopile.
Learn More About Studying Corrosion with COMSOL Multiphysics®
- Try modeling the examples featured in this blog post:
- Read other blog posts related to simulating corrosion:
Editor’s note: This blog post was updated on February 5, 2021.





Comments (0)